PPO#
PPO(Proximal Policy Optimization)算法出自Schulman et al.,在微调大模型中,该算法通过最大化以下目标函数来优化模型参数:
$$
\mathcal J_{PPO}(\theta)=\mathbb E_{[q\sim P(Q),o\sim \pi_{\theta_{old}}(O\vert q)]}\frac{1}{\vert o\vert}\sum_{t=1}^{\vert o\vert}\min\left[\frac{\pi_\theta(o_t\vert q,o_{< t})}{\pi_{\theta_{old}}(o_t\vert q,o_{< t})}A_t,\text{clip}\left(\frac{\pi_\theta(o_t\vert q,o_{< t})}{\pi_{\theta_{old}}(o_t\vert q,o_{< t})},1-\epsilon,1+\epsilon\right)A_t\right]
$$
其中优势函数$A_t$通过使用GAE(Generalized Advantage Estimation)算法计算得到:
$$
r_t=r_\phi(q,o_{1:\vert o\vert}) - \beta \log\frac{\pi_\theta(o_t\vert q,o_{< t})}{\pi_{ref}(o_t\vert q,o_{< t})}
$$
$$
A_t=\delta_t + (\gamma\lambda)\delta_{t+1} + (\gamma\lambda)^2\delta_{t+2}+\cdots=\sum_{l=0}^\infty (\gamma\lambda)^l\delta_{t+l}
$$
$$
\delta_t=r_t+\gamma V(s_{t+1}) - V(s_t)
$$
针对大模型微调的场景,$q$为问题(或者prompt),假设其最大长度为max_prompt_len,生成的$o_{1:\vert o\vert}$为答案(或者generation sentence),假设其最大长度为max_seq_len。上式中$r_t$为奖励,$r_\phi$为reward model(PPO优化中参数不更新),该模型输入$q$和$o_{1:\vert o\vert}$得到每个句子的最后一个有效token上的reward score,因此$r_\phi(q,o_{1:\vert o\vert})$的维度可以记作(bs,)($bs$为ppo批量大小),KL惩罚项使用估计项$\log\frac{\pi_\theta(\cdot)}{\pi_{ref}(\cdot)}$,该项得到的维度为(bs, max_seq_len),因此最终的奖励向量$r_t$维度为(bs, max_seq_len)。接着看一下DeepSpeed中对优势函数和回报实现的代码:
1
2
3
4
5
6
7
8
9
10
11
12
|
def get_advantages_and_returns(self, values, rewards):
lastgaelam = 0
advantages_reversed = []
max_seq_len = rewards.shape[-1]
for t in reversed(range(max_seq_len)):
nextvalues = values[:, t + 1] if t < max_seq_len - 1 else 0.0
delta = rewards[:, t] + self.gamma * nextvalues - values[:, t]
lastgaelam = delta + self.gamma * self.lam * lastgaelam
advantages_reversed.append(lastgaelam)
advantages = torch.stack(advantages_reversed[::-1], dim=1)
returns = advantages + values
return advantages, returns
|
经过一次for循环得到的分别是(令max_seq_len为$\vert o\vert$):
$$
\begin{align}
A_{t=\vert o\vert - 1}&=\delta_{\vert o\vert - 1}A_{t=\vert o\vert - 2}\\
&=(\gamma\lambda)\delta_{\vert o\vert - 1} + \delta_{\vert o\vert -2}A_{t=\vert o\vert -3}\\
&=(\gamma\lambda)^2\delta_{\vert o\vert - 1} + (\gamma\lambda)\delta_{\vert o\vert -2} + \delta_{\vert o\vert - 3}\cdots A_{t=0}\\
&=(\gamma\lambda)^{\vert o\vert -1}\delta_{\vert o\vert - 1} + (\gamma\lambda)^{\vert o\vert -2}\delta_{\vert o\vert -2} + \cdots + (\gamma\lambda)\delta_{1} + \delta_0
\end{align}
$$
经过翻转后,得到优势向量$A_t=[A_{t=0}, A_{t=1},\cdots, A_{t=\vert o\vert - 1}]$,向量维度为(bs, max_seq_len)
GRPO#
GRPO(Group Relative Policy Optimization)算法出自Shao et al.,其优化目标如下:
$$
\begin{align*}
\mathcal{J}_{\text{GRPO}}(\theta) &= \mathbb{E}\left[q \sim P(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(O|q)\right]\\
&=\frac{1}{G} \sum_{i=1}^G \left\{
\min \left[
\frac{\pi_{\theta}(o_i | q)}{\pi_{\theta_{\text{old}}}(o_i | q)} A_i,
\text{clip}\left( \frac{\pi_{\theta}(o_i | q)}{\pi_{\theta_{\text{old}}}(o_i | q)}, 1 - \epsilon, 1 + \epsilon \right) A_i
\right]
- \beta \mathbb D_{\text{KL}}[\pi_{\theta} \| \pi_{\text{ref}}]
\right\}\\
&=\frac{1}{G} \sum_{i=1}^G\frac{1}{\vert o_i\vert}\sum_{t=1}^{\vert o_i\vert}\left\{\min\left[\frac{\pi_\theta(o_{i,t}\vert q,o_{i,< t})}{\pi_{\theta_{old}}(o_{i,t}\vert q, o_{i,< t})}\hat A_{i,t},\ \text{clip}\left(\frac{\pi_\theta(o_{i,t}\vert q,o_{i,< t})}{\pi_{\theta_{old}}(o_{i,t}\vert q,o_{i, < t})},1-\epsilon,1+\epsilon\right)\hat A_{i,t}\right] - \beta\mathbb D_{KL}[\pi_\theta\Vert\pi_{\text{ref}}]\right\}
\end{align*}
$$
$$
D_{\text{KL}}(\pi_{\theta} \| \pi_{\text{ref}}) =
\frac{\pi_{\text{ref}}(o_{i, t} | q, o_{i, < t})}{\pi_{\theta}(o_{i, t} | q, o_{i, < t})}
- \log \frac{\pi_{\text{ref}}(o_{i, t} | q, o_{i, < t})}{\pi_{\theta}(o_{i, t} | q, o_{i, < t})} - 1,
$$
$$
\hat A_{i,t}=A_i = \frac{r_i - \text{mean}(\{r_1, r_2, \cdots, r_G\})}{\text{std}(\{r_1, r_2, \cdots, r_G\})}.
$$
DAPO#
Yu et al.提出了DAPO(Decouple Clip and Dynamic sAmpling Policy Optimization)算法,该算法基于GRPO算法提出了四点改进,其优化目标如下:
$$
\begin{align*}
\mathcal J_{DAPO}(\theta)&=\mathbb E_{(q,a)\sim\mathcal D,\{o_i\}_{i=1}^G\sim\pi_{\theta_{old}}(\cdot\vert q)}\left\{\frac{1}{\sum_{i=1}^G\vert o_i\vert}\sum_{i=1}^G\sum_{t=1}^{\vert o_i\vert}\min\left[r_{i,t}(\theta)\hat A_{i,t},\text{clip}\left(r_{i,t}(\theta),1-\epsilon_{\text{low}},1+\epsilon_{\text{high}}\right)\hat A_{i,t}\right]\right\}\\
% & \text{s.t.}\quad 0 < \vert \{o_i\vert \text{is\_equivalent}\}
& \text{s.t.}\quad 0 < \left\vert \{o_i\ \vert\ \text{is\_equivalent}(a, o_i)\}\right\vert < G,
\end{align*}
$$
$$
r_{i,t}(\theta)=\frac{\pi_\theta(o_{i,t}\vert q,o_{i,< t})}{\pi_{\theta_{old}}(o_{i,t}\vert q,o_{i, < t})},\quad \hat A_{i,t}=\frac{R_i-\text{mean}(\{R_i\}_{i=1}^G)}{\text{std}(\{R_i\}_{i=1}^G)}
$$
首先作者移除了GRPO算法中的KL散度惩罚,作者认为对于训练long-CoT推理模型,actor model的输出分布与ref model的输出分布自然存在较大差异,没有必要设置KL散度限制。其次对于DAPO,作者采用基于规则的奖励模型,对于可验证任务(automated throrem proving、computer programming、mathematics competition),作者使用如下奖励函数,其中$\hat y$是预测答案,$y$是标准答案。
$$
R(\hat y, y)=
\begin{cases}
1,& \text{is\_equivalent}(\hat y, y)\\
-1,& \text{otherwise}
\end{cases}
$$
Insights#
接着,作者针对GRPO的理论缺陷提出了四点比较有意思的insights,每个insight对原本算法的改动都很小,但存在一定效果的提升。
TLDR:将原先的clip函数的上下界单独设置,而不是统一设置。
Motivation:对于生成的sentences,其中大部分token的概率值都较低,因此使用一个较低的$\epsilon$(一般算法设置$\epsilon=0.2$)对于这些低概率token的提升非常有限,比如$\pi_{\theta_{old}}(o_i\vert q)=0.01$,当$\epsilon=0.2$时,$\pi_{\theta}(o_i\vert q)$最大值只能为0.012。简单来说就是大部分token的概率值均偏低(< 0.2),而低概率值的token更容易被clip(原因如上所述),作者认为这限制了模型对低概率token的提升,从而限制了整个模型的生成多样性。作者论文中实验设置了$\epsilon_{\text{low}}=0.2$,$\epsilon_{\text{high}}=0.28$。
TLDR:让每批采样的answer不能全部正确也不能全部错误。
Motivation:当每批采样的answer全部正确或全部错误时,计算得到的优势$\hat A_{i,t}=0$,这导致梯度值为零,那导致模型在这一步上等价于没有学习,降低了采样效率。因此作者在每个step会多次采样(理解为对同一批prompt生成answer),直到answer的平均准确率介于0和1之间。
- Token-Level Policy Gradient Loss
TLDR:对一批生成样本中的每个token采用相同的损失贡献比例,而不是每个样本各自先按长度归一化损失再平均每个样本的损失。
Motivation:作者认为GRPO中的损失归一方式对long-CoT RL场景不友好,在GRPO中,每批样本中长样本的每个token贡献的损失比重会低于短样本的每个token贡献的损失比重,这会导致两个问题:1)对于高质量的长样本,这会阻碍模型学习这类样本的推理模式,2)对于低质量的长样本(出现重复,垃圾话),样本层级的损失计算也无法有效对这些样本进行惩罚。
TLDR:设置一个最大生成长度,对超出长度的样本进行惩罚。
Motivation:传统RL训练,对于过长样本会直接截断,但这种直接截断会带来噪音影响训练过程,因为一个合理但过长的样本被截断显然会影响模型训练。作者首先尝试将每批数据中被截断的损失mask掉,发现这会提升训练稳定性且提升模型性能。进一步地,作者设计了SoftOverlongPunishment,计算方式如下。这个惩罚性奖励被添加到原始基于规则的正确性奖励中一起计算总奖励。
$$
R_{\text{length}}(y)=
\begin{cases}
0,& \vert y\vert \le L_{\text{max}} - L_{\text{cache}} \\\\
\frac{(L_{\text{max}}-L_{\text{cache}})-\vert y\vert}{L_{\text{cache}}},& L_{\text{max}}-L_{\text{cache}} < \vert y\vert\le L_{\text{max}}\\\\
-1,& L_{\text{max}} < \vert y\vert
\end{cases}
$$
Dr. GRPO#
Liu et al.提出Dr. GRPO,该工作指出GRPO算法存在的一些bias,并且这些bias可能导致了GRPO算法随着训练步数增加,生成answer长度不断增加的现象(包括出现aha moment)。该工作提出了两个bias:
-
Response-level length bias:源于对损失除了$\vert o_i\vert$,这样,对于正优势($\hat A_{i,t}> 0$,correct response),该偏差使得较短的response的梯度更大($\vert o_i\vert$更小),从而导致策略倾向更简洁的正确回答。相反,对于负优势($\hat A_{i,t}< 0$,incorrect response),该偏差使得较长的response的梯度更大($\vert o_i\vert$更大),从而导致策略倾向更复杂的错误回答。
-
Question-level difficulty bias:源于计算优势时对奖励偏差除了$\text{std}(\lbrace r_1,\cdots,r_G\rbrace)$。因此对于某个特定question,如果其answers容易得到较低的variance,那么这批answer的梯度会更大。通常来说优势归一化在常规RL算法中是在一整个batch上进行,而GRPO在每个question上进行归一化,导致对于不同question的answer,其梯度值可能会有较大差异。
对此,作者移除了$\frac{1}{\vert o_i\vert}$和$\text{std}(\lbrace r_1,\cdots,r_G\rbrace)$,并将$\vert o_i\vert$替换为一个固定值。
$$
\begin{align*}
\mathcal{J}_{\text{GRPO}}(\theta) &= \mathbb{E}\left[q \sim P(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(O|q)\right]\\
&=\frac{1}{G} \sum_{i=1}^G\textcolor{red}{\frac{1}{\vert o_i\vert}}\sum_{t=1}^{\vert o_i\vert}\left\{\min\left[\frac{\pi_\theta(o_{i,t}\vert q,o_{i,< t})}{\pi_{\theta_{old}}(o_{i,t}\vert q, o_{i,< t})}\hat A_{i,t},\ \text{clip}\left(\frac{\pi_\theta(o_{i,t}\vert q,o_{i,< t})}{\pi_{\theta_{old}}(o_{i,t}\vert q,o_{i, < t})},1-\epsilon,1+\epsilon\right)\hat A_{i,t}\right] - \beta\mathbb D_{KL}[\pi_\theta\Vert\pi_{\text{ref}}]\right\}
\end{align*}
$$
$$
\hat A_{i,t}=A_i = \frac{r_i - \text{mean}(\{r_1, r_2, \cdots, r_G\})}{\textcolor{red}{\text{std}(\{r_1, r_2, \cdots, r_G\})}}.
$$
Insights#
作者对比了GRPO与Dr. GRPO,发现随着训练进行,Dr. GRPO的平均生成长度不会一直增加而是收敛。两者回答正确的answer长度均收敛,但不正确的answer长度中,GRPO不断增加而Dr. GRPO收敛甚至有所下降。两者最终性能表现相当。这证明了Dr. GRPO有更高的token efficiency。
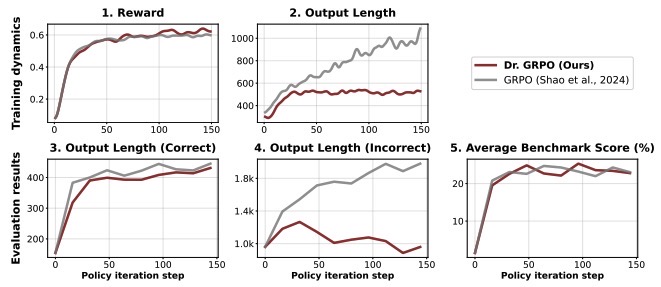
图1:GRPO vs. Dr. GRPO
Skywork Open Reasoner Series#
Blog链接:He et al.
7B数学模型在AIME24上取得69.8%准确率(avg@8)
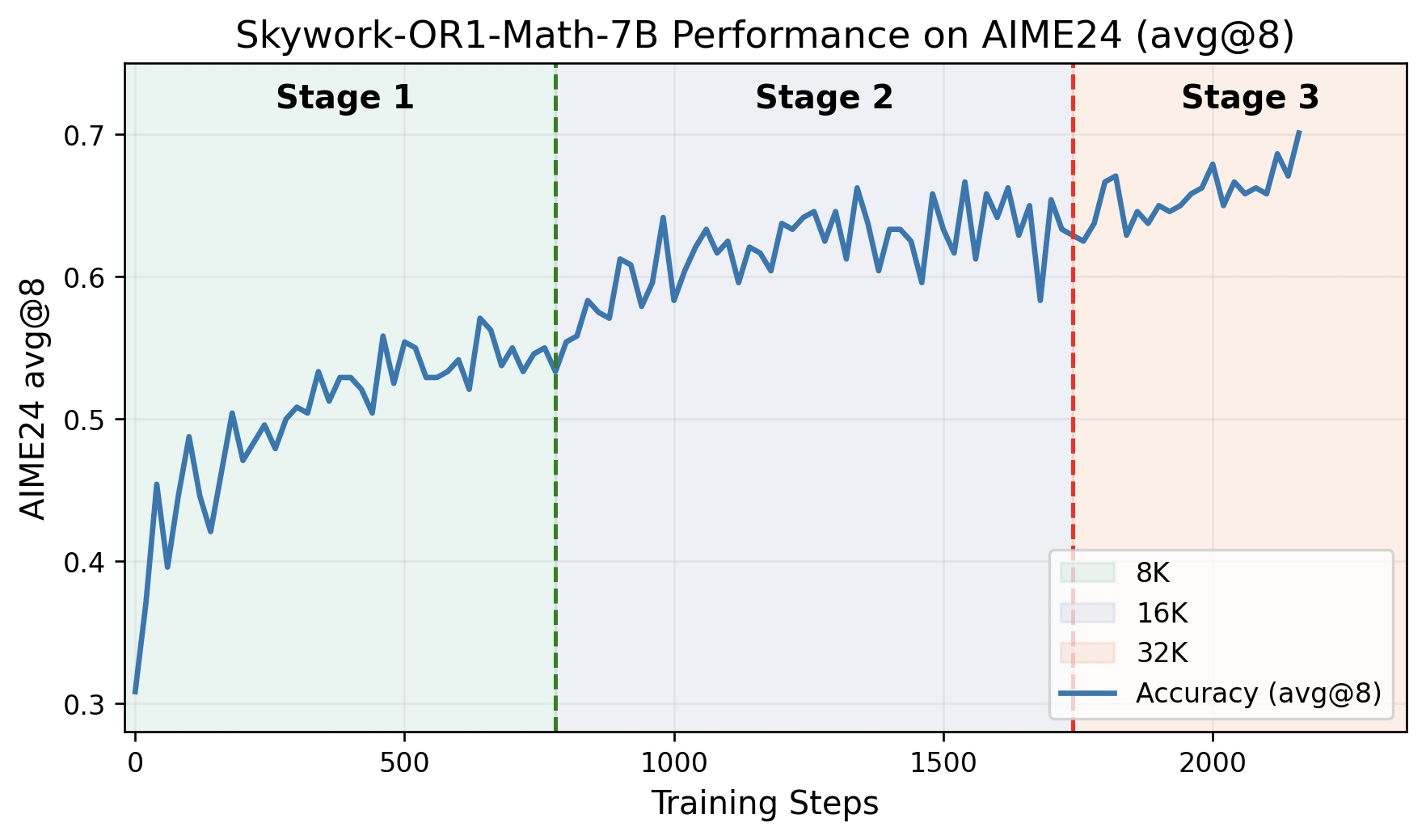
图2:Skywork-OR1-Math-7B Performance on AIME24(avg@8)
Data Preparation#
Multi-stage GRPO with Adaptive Entropy Control#
优化目标函数如下:
$$
\mathcal J(\theta)=\frac{1}{T_k}\sum_{i\in\mathcal T_k}\sum_{j=1}^M\left\{\sum_{t=0}^{\vert y_{ij}-1\vert}\min\{\rho_t^{ij}(\theta)\hat A_{ij},\text{clip }(\rho_t^{ij}(\theta),1-\epsilon,1+\epsilon)\hat A_{ij}\}-\alpha_k\mathbb H_t^{ij}(\theta)\right\}
$$
$$
\hat A_{ij}=\frac{r_{ij}-\text{mean }(\textbf{r}_i)}{\text{std }(\textbf{r}_i)}
$$
$$
\rho_{t}^{ij}(\theta)=\frac{\pi_\theta(a_t^{(ij)}\vert s_t^{(ij)})}{\pi_{\theta_{k}}(a_t^{(ij)}\vert s_t^{(ij)})}
$$
$$
s_t^{(ij)}=(x_i,a_0^{(ij)},\cdots,a_{t-1}^{(ij)})
$$
$$
T_k=\sum_{i\in\mathcal T_k}\sum_{j=1}^M\vert y_{ij}\vert
$$
$$
\mathbb H_{t}^{ij}(\theta)=\mathcal H(\pi_\theta(\cdot\vert s_t^{(ij)}))=-\sum_{a_t^{(ij)}\in\mathcal V}\pi_\theta(a_t^{(ij)}\vert s_t^{(ij)})\log\pi_\theta(a_t^{(ij)}\vert s_t^{(ij)})
$$
相较于GRPO的主要改动:
- 去除KL散度惩罚,这与DAPO,Dr. GRPO中的做法相一致。
- 增加生成熵的约束,防止模型熵爆炸。
- 归一化采用batch内所有数据归一化,即最后损失项乘了 $\frac{1}{\sum_{i\in\mathcal T_k}\sum_{j=1}^M}$,其中$\mathcal T_k$为当前batch中所有prompt的集合,$M$为每个prompt的生成answer数量。
此外在训练数据处理上,作者针对long cot模型的训练加入了以下优化:
Multi-Stage Training#
作者训练分为3个阶段,逐渐增大最大生成长度,主要用来减少训练时间,同时保证最终模型的性能。当前一个阶段性能收敛时进入下一个阶段(但感觉得通过实验来选取经验值,如第一阶段训练多少个step这种)。
| Stage1 |
Stage2 |
Stage3 |
| 8K |
16K |
32K |
On the Issue of Truncated Samples#
作者针对最大生成长度限制内,出现生成过长导致截断的问题,提出了Advantage Mask For Truncated方法,并给出了两种方案:
$$
\hat A_{ij}=
\begin{cases}
\frac{r(x_i,y_{ij})-\text{mean}(\hat {\mathbb R}_i)}{\text{std}(\hat{\mathbb R}_i)}& \vert y_{ij}\vert \le T_{\text{max}}\\\\
0,& \vert y_{ij}\vert > T_{\text{max}}
\end{cases}
$$
其中$\hat{\mathbb R}_i$为没被阶段的answer的奖励集合。
$$
\hat A_{ij}=
\begin{cases}
\frac{r(x_i,y_{ij})-\text{mean}({\mathbb R}_i)}{\text{std}({\mathbb R}_i)}& \vert y_{ij}\vert \le T_{\text{max}}\\\\
0,& \vert y_{ij}\vert > T_{\text{max}}
\end{cases}
$$
其中$\mathbb R_i$为所有answer的奖励集合。
实验结果发现两个mask效果都不如不加mask,因此作者没有使用这两种mask。
Adaptive Entropy Control#
作者发现生成熵损失对超参数$\alpha_k$和训练数据分布都非常敏感,因此提出adaptive entropy control的方法。具体来说,作者设置一个熵阈值tgt-ent(即想要模型保持的生成熵水平)以及一个变化量$\vartriangle$。设置$\alpha_k$初始值为0,每个step前,用当前actor模型计算当前batch的平均生成熵e,如果e小于tgt-ent,那么增加$\alpha_k: \alpha_k=\alpha_k+\vartriangle$。考虑到增加熵损失会带来训练不稳定,因此当e大于tgt-ent时,该step不会启用熵损失,即理解为$\alpha_k=0$。实验中,作者设置tgt-ent=0.2,$\vartriangle$=0.005。
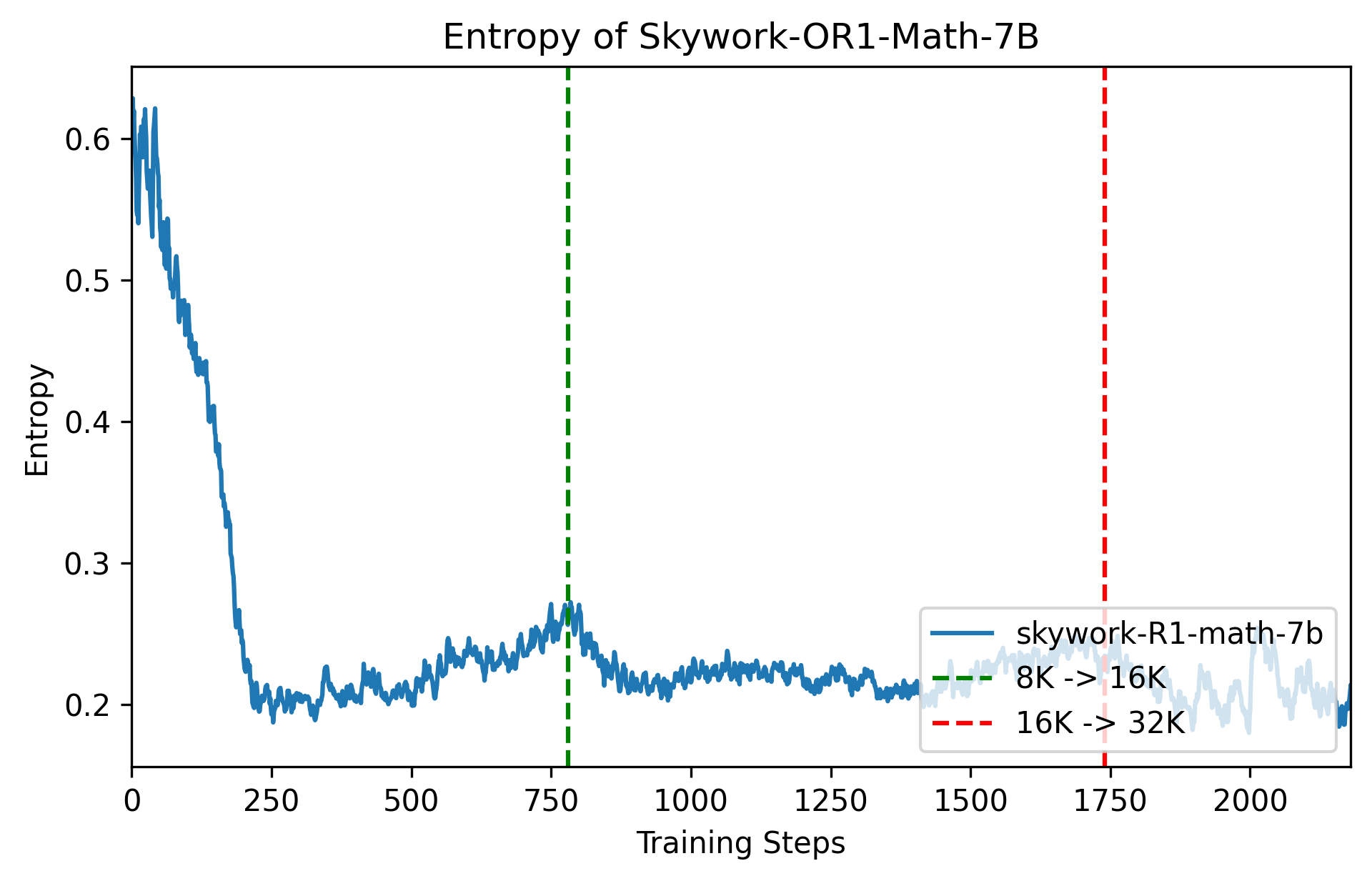
图3:Adaptive entropy control, tgt-ent=0.2, $\vartriangle$=0.005
这部分的大概作用就是,不设置生成熵损失或者超参数$\alpha_k$比较小的时候,在较少的训练step后,模型的生成熵便会降到很低接近0的值,这对模型的探索能力起到负面影响,同时作者发现,当$\alpha_k$设置较大时(> 1e-3),在较少训练step后,模型的生成熵就爆炸了,因此可以理解,提高$\alpha_k$会在一定程度上扰乱模型的生成熵防止其快速收敛。训练的最终目的是让模型的生成熵稳定在一个较低水平但不是接近0的值,因此这种Adaptive Entropy Control方法可以很好地解决这个问题。当前估计的熵值e较小则提高$\alpha_k$,当前估计的熵值e较大则不启用熵损失,让模型自然训练降低生成熵即可。
References#
[1] Yu et al. “DAPO: An Open-Source LLM Reinforcement Learning System at Scale” arXiv preprint arXiv:2503.14476 (2025).
[2] Shao et al. “DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models” arXiv preprint arXiv:2402.03300 (2024).
[3] Schulman et al. “Proximal Policy Optimization Algorithms” arXiv preprint arXiv:1707.06347 (2017).
[4] Liu et al. “Understanding R1-Zero-Like Training: A Critical Perspective” Github 2025.
[5] He et al. “Skywork Open Reasoner Series” Notion Blog 2025.


