From OneRec to RL

最近读到LLM做推荐比较火热的工作oncrec，感觉其整体思路挺有意思，这篇blog记录一下

OneRec

在25年2月份快手团队先推出了onerec [1]，这个版本使用一个encoder-decoder模型架构，同时在decoder使用moe架构搭建了整个模型框架，然后在训练中分别使用Next Token Prediction损失冷启动模型，后使用一个RM构造偏序数据并基于DPO做进一步微调。

首先最关心的一个问题是，训练数据是什么呢，仔细看后发现，作者直接把所有的视频先用一个视频编码模型向量化，然后把所有的视频特征向量做了三层聚类得到三层码本，最后每一个视频变成3串编码后的数字（比如12-34-56）。

Balanced K-means Clustering

为了得到类别均衡的聚类结果，作者提出了balanced k-means算法，这块使用贪心的方式，强行让每个类别数量均衡。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

def balanced_kmeans(V, K, tol=1e-6):
    V = np.array(V)
    N = V.shape[0]
    w = N // K if N % K == 0 else N // K + 1  # 计算每个聚类的目标大小 w
    
    initial_indices = np.random.choice(N, K, replace=False)
    centroids = V[initial_indices].copy()
    
    while True:
        prev_centroids = centroids.copy()
        
        unassigned_indices = np.arange(N)
        for k in range(K):
            if len(unassigned_indices) == 0:
                break
                
            u_vectors = V[unassigned_indices]
            distances = np.sum((u_vectors - centroids[k])**2, axis=1)
            sorted_local_indices = np.argsort(distances)

            count = min(w, len(unassigned_indices))
            assigned_local_indices = sorted_local_indices[:count]
            assigned_global_indices = unassigned_indices[assigned_local_indices]

            if len(assigned_global_indices) > 0:
                centroids[k] = np.mean(V[assigned_global_indices], axis=0)
            
            # 更新未分配集合
            mask = np.ones(len(unassigned_indices), dtype=bool)
            mask[assigned_local_indices] = False
            unassigned_indices = unassigned_indices[mask]
            
        # 判断连续两次迭代的码本是否收敛（在 tol 误差范围内一致）
        if np.allclose(prev_centroids, centroids, atol=tol):
            break
        
    return centroids

基于上述算法，作者还引入了多轮聚类，当所有视频的特征向量$[v_1,v_2,\cdots,v_N]$第一轮聚类收敛得到第一层码本$[c^1_1,c^1_2,\cdots,c^1_K]$，接着按聚类中心顺序分配特征向量后，每个向量分配到一个中心，用所有特征向量减去对应中心向量得到每个特征向量的一级残差向量$[r^1_1,r^1_2,\cdots,r^1_N]$，对一级残差向量同样做一遍balanced-kmeans聚类，得到第二层码本$[c^2_1,c^2_2,\cdots,c^2_K]$。接着给一级残差向量分配二级中心后，用一级残差向量减去对应二级中心得到二级残差向量$[r^2_1,r^2_2,\cdots,r^2_N]$，再来一轮聚类得到三级码本$[c^3_1,c^3_2,\cdots,c^3_K]$。在对所有二级残差向量分配三级中心，至此，所有的原始视频都能分配到一组三级标签：$idx(c^1_i)-idx(c^2_j)-idx(c^3_k)$，也就完成了从视频本身到语义标签的转化。

Session-wise List Generation

基于上面对海量视频库都打上三级标签，然后对于单个用户，基于滑动窗口的方式任意截取连续24h用户观看视频列表，然后做切分为$[user, assistant]$，简单理解就是输入和输出，用输入的观看视频预测用户可能观看的视频输出。当然在$assistant$的视频会有一些比较高的要求，比如观看时长，点赞转发等行为的支撑。对海量用户构建了海量这样的数据对后，采用类似SFT的方法对模型做训练，不过用的是encoder-decoder架构的模型，个人理解完全可以用LLM常规的decoder-only来做。

这个方法感觉还是比较excitement，团队抛弃了用户本身的所有信息，只从用户行为出发，对结果做预测，是一个比较纯粹的方法。

Gradient Analysis of PPO, ECPO, GBPO

其实在onerec 2月份版本团队还做了相关reward model的工作，并用reward model筛选偏序数据对，做了一些DPO的工作，但整体来看不是特别主流了，尤其是在25年底，基本做法还是RL为主。后面发现这个onerec还有v1[2]和v2版本[3]，对onerec 2月份版本做挺多改进的，首先v2版本中模型架构上换了decoder-only架构配合moe，其次在训练上，放弃了DPO选择了RL，分别在v1版本和v2版本提出了较新的训练范式ECPO和GBPO。下面对v1版本提出的ECPO，v2版本提出的GBPO以及经典PPO的梯度做简单分析。

PPO

$$ J_{PPO}(\theta)=\min\left[\frac{\pi_\theta}{\pi_{old}}\cdot A, \text{clip}(\frac{\pi_\theta}{\pi_{old}},1-\epsilon,1+\epsilon)\cdot A\right] $$

$A \ge 0$

$$ \begin{align} J_{PPO}(\theta)&=\begin{cases} \frac{\pi_\theta}{\pi_{old}}\cdot A&,0\le\frac{\pi_\theta}{\pi_{old}}\le 1+\epsilon \\ (1+\epsilon)\cdot A&,\frac{\pi_\theta}{\pi_{old}}> 1+\epsilon \end{cases} \\ \\ \nabla_\theta J_{PPO}(\theta)&=\begin{cases} \frac{\pi_\theta}{\pi_{old}}\cdot A\cdot\nabla_\theta\log\pi_\theta&,0\le\frac{\pi_\theta}{\pi_{old}}\le 1+\epsilon \\ 0&, \frac{\pi_\theta}{\pi_{old}}> 1+\epsilon \end{cases} \end{align} $$

$A < 0$

$$ \begin{align} J_{PPO}(\theta)&=\begin{cases} (1-\epsilon)\cdot A &,0\le\frac{\pi_\theta}{\pi_{old}}\le 1-\epsilon \\ \frac{\pi_\theta}{\pi_{old}}\cdot A&,\frac{\pi_\theta}{\pi_{old}}> 1-\epsilon \end{cases} \\ \\ \nabla_\theta J_{PPO}(\theta)&=\begin{cases} 0&,0\le\frac{\pi_\theta}{\pi_{old}}\le 1-\epsilon \\ \frac{\pi_\theta}{\pi_{old}}\cdot A\cdot\nabla_\theta\log\pi_\theta &,\frac{\pi_\theta}{\pi_{old}}> 1-\epsilon \end{cases} \end{align} $$

梯度项包含了$\frac{\pi_\theta}{\pi_{old}}$，$A$和$\nabla_\theta\log\pi_\theta$，正常来说$A$为优势函数，通常不会有爆炸的情况，而对于$\nabla_\theta\log\pi_\theta$，定义$z_\theta$为模型输出层输出的logits，通过偏导拆解分析：

$$ \nabla_\theta\log\pi_\theta=\frac{\partial\log\pi_\theta}{\partial\theta}=\frac{\partial\log\pi_\theta}{\partial z_\theta}\cdot\frac{\partial z_\theta}{\partial \theta} $$

其中$\pi_\theta=\frac{e^{z_\theta}}{\sum_j e^{z_j}}$，所以$\frac{\partial\log\pi_\theta}{\partial z_\theta}=\frac{\partial(z_\theta-\log\sum_j e^{z_j})}{\partial z_\theta}=\mathbf{1}-\frac{\partial\log\sum_j e^{z_j}}{\partial z_\theta}=\mathbf{1}-\frac{1}{\sum_j e^{z_j}}e^{z_\theta}=\mathbf{1}-\pi_\theta$，带入上面的公式得到：

$$ \nabla_\theta\log\pi_\theta=(\mathbf{1}-\pi_\theta)\cdot\frac{\partial z_\theta}{\partial\theta} $$

其中$|\mathbf{1}-\pi_\theta|\le 1$，而$\frac{\partial z_\theta}{\partial\theta}$为反向传播每层参数的梯度，通常来说由于现在的模型结构每层都有使用RMSNorm或者LayerNorm，这一项在统计上是比较稳定的。

所以综上分析容易诱发梯度爆炸的项只有$\frac{\pi_\theta}{\pi_{old}}$，对于$A\ge 0$的情况，会发现该比值过高的时候梯度直接被clip归零了，因此不会存在梯度爆炸问题。但对于$A< 0$的情况，当$\frac{\pi_\theta}{\pi_{old}}\ge 1+\epsilon$时，虽然在公式上先被clip了，但是由于PPO这种“悲观的min”设计，最终对于负样本，梯度会全盘接受，所以在负优势的场景，如果该比值过大时，会诱发梯度爆炸而训练崩溃。

ECPO

$$ J_{ECPO}(\theta)=\frac{1}{G}\sum_{i=1}^G\min\left(\frac{\pi_\theta}{\pi_{old}^\prime}\cdot A_i,\text{clip}\left(\frac{\pi_\theta}{\pi^\prime_{old}},1-\epsilon,1+\epsilon\right)\cdot A_i\right) $$

$$ \pi^\prime_{old}=\max\left(\frac{\text{sg}(\pi_\theta)}{1+\epsilon+\delta},\pi_{old}\right),\quad\delta> 0 $$

ECPO在GRPO基础上，修改了$\pi_{old}$的定义，针对单个rollout case分析，在上面PPO梯度存在问题的场景（$A< 0,\frac{\pi_\theta}{\pi_{old}}> 1-\epsilon$）

$$ \nabla_\theta J_{ECPO}(\theta)=\frac{\pi_\theta}{\pi_{old}^\prime}\cdot A\cdot\nabla_\theta\log\pi_\theta,\quad A< 0,\frac{\pi_\theta}{\pi_{old}^\prime}> 1-\epsilon $$

这时候分情况讨论，如果$\pi_{old}\ge\frac{\text{sg}(\pi_\theta)}{1+\epsilon+\delta}$，那么：

$$ \nabla_\theta J_{ECPO}(\theta)=\frac{\pi_\theta}{\pi_{old}}\cdot A\cdot\nabla_\theta\log\pi_\theta\le(1+\epsilon+\delta)\cdot A\cdot\nabla_\theta\log\pi_\theta $$

如果$\pi_{old}<\frac{\text{sg}(\pi_\theta)}{1+\epsilon+\delta}$：

$$ J_{ECPO}(\theta)=\frac{(1+\epsilon+\delta)\pi_\theta}{\text{sg}(\pi_\theta)}\cdot A, $$

$$ \nabla_\theta J_{ECPO}(\theta)=\frac{(1+\epsilon+\delta)\nabla_\theta\pi_\theta}{\pi_\theta}\cdot A=(1+\epsilon+\delta)\cdot A\cdot\nabla_\theta\log\pi_\theta $$

因此，整体梯度都限制在$(1+\epsilon+\delta)\cdot A\cdot\nabla_\theta\log\pi_\theta$范围内，一定程度缓解梯度爆炸问题。

GBPO

$$ J_{GBPO}(\theta)=\frac{1}{G}\sum_{i=1}^G\frac{\pi_\theta}{\pi^\prime_{old}}\cdot A_i $$

$$ \pi_{old}^\prime=\begin{cases} \max(\pi_{old},\text{sg}(\pi_\theta)),&A_i\ge 0 \\ \max(\pi_{old},1-\text{sg}(\pi_\theta)),& A_i< 0 \end{cases} $$

整体上，GBPO移除了PPO的clip策略，因为该策略会导致很多样本梯度为0，导致学习困难。

对于单rollout case分析

$A\ge 0$

$$ \begin{align} J_{GBPO}(\theta)&=\begin{cases} \frac{\pi_\theta}{\pi_{old}}\cdot A,&\pi_{old}\ge\text{sg}(\pi_\theta) \\ \frac{\pi_\theta}{\text{sg}(\pi_\theta)}\cdot A,& \pi_{old}<\text{sg}(\pi_\theta) \end{cases} \\ \nabla_\theta J_{GBPO}(\theta)&=\begin{cases} \frac{\pi_\theta}{\pi_{old}}\cdot A\cdot\nabla_\theta\log\pi_\theta,&\pi_{old}\ge\text{sg}(\pi_\theta) \\ A\cdot\nabla_\theta\log\pi_\theta,&\pi_{old}<\text{sg}(\pi_\theta) \end{cases} \end{align} $$

$A< 0$

$$ \begin{align} J_{GBPO}(\theta)&=\begin{cases} \frac{\pi_\theta}{\pi_{old}}\cdot A,&\pi_{old}\ge 1-\text{sg}(\pi_\theta) \\ \frac{\pi_\theta}{1-\text{sg}(\pi_\theta)}\cdot A,&\pi_{old}< 1-\text{sg}(\pi_\theta) \end{cases} \\ \nabla_\theta J_{GBPO}(\theta)&=\begin{cases} \frac{\pi_\theta}{\pi_{old}}\cdot A\cdot\nabla_\theta\log\pi_\theta,&\pi_{old}\ge 1-\text{sg}(\pi_\theta) \\ \frac{\pi_\theta}{1-\pi_\theta}\cdot A\cdot\nabla_\theta\log\pi_\theta,&\pi_{old}< 1-\text{sg}(\pi_\theta) \end{cases} \end{align} $$

整体上，GBPO对于正负样本，都不会存在大量梯度为0的场景，且对于负样本场景，由于$\pi_\theta$基本会比较小，$\frac{\pi_\theta}{1-\pi_\theta}\ll 1$，所以GBPO的梯度更加稳定，受优势变化的影响更小。

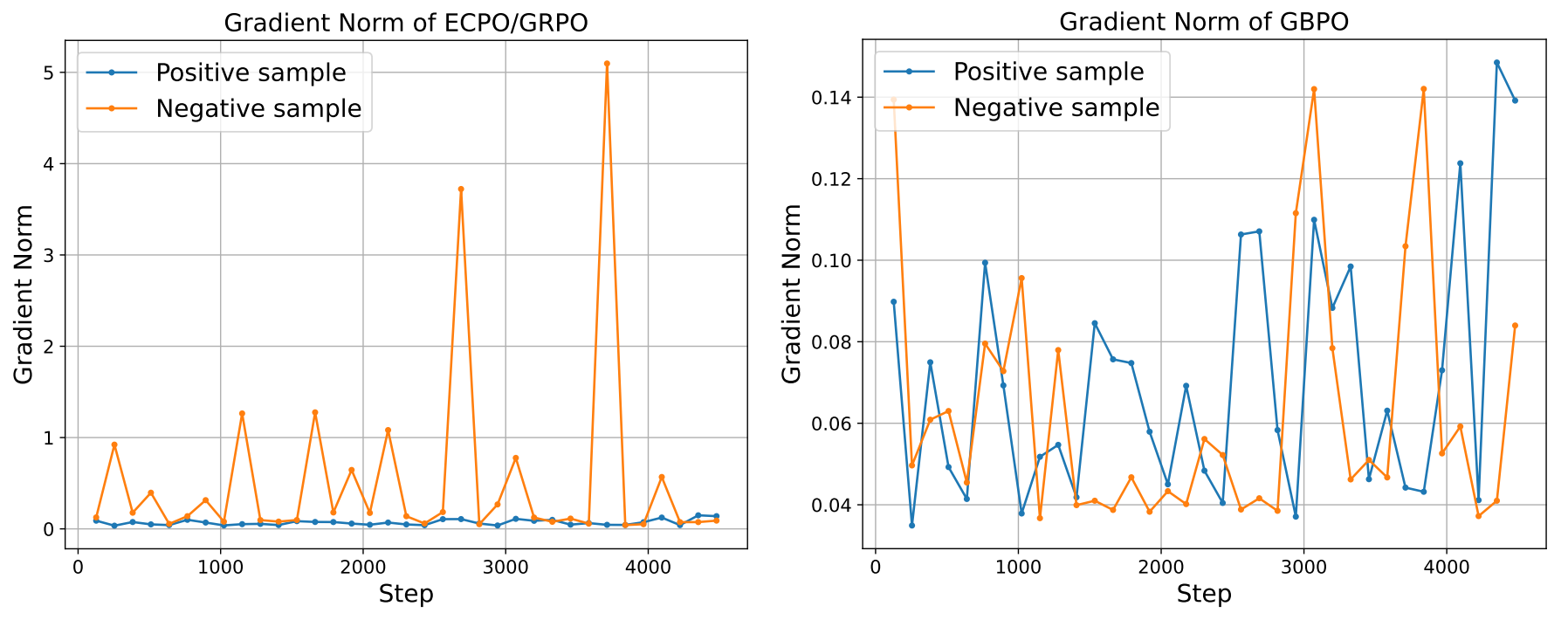
作者对比了ECPO/GRPO和GBPO的梯度分布情况，发现对于负样本，传统基于clip的强化学习方法，梯度跳动明显，但对于GBPO，正负样本的梯度分布都比较稳定。

References